Relatividade do tempo e Risco
Suponha que você esteja jogando cartas, neste exemplo vamos estar jogando jogo de buraco ou Canastrão, a pergunta então é:
Qual a probabilidade de você sair na primeira rodada com uma sequência completa do naipe de copas de As à Valete?
Normalmente todos irão responder que é muito baixa, que em princípio é uma afirmação correta, olhando se no curto espaço de tempo, agora se formos considerar no horizonte de análise um período de tempo muito grande, a probabilidade não é baixa, porque num tempo infinitamente grande todas as possibilidades acontecem, ou seja, longos períodos de tempo é suficiente para que eventos improváveis aconteçam.
O melhor exemplo disso é a existência da vida, acima de tudo vida inteligente. Para existir vida inteligente na terra foram necessários 5 milhões de anos de existência do sistema solar e 10 milhões de existência do universo.
Quando estivermos falando de gestão de risco, é preciso levar em consideração que eventos improváveis sobem na escala de probabilidade no decorrer do tempo toda vez que estivermos avaliando cenários de tempo muito longo.
Vejamos um exemplo; atualmente a probabilidade de acidentes aéreos é de 10 fatalidades por milhão de passageiros embarcados por ano, ou seja, olhando este evento com o enfoque de um único vôo, podemos concluir que as chances de acontecer são remotas. Por outro lado, considerando um horizonte de 100 anos, estaríamos falando em algo em torno de milhares de fatalidades, se considerado as estatísticas atuais.
Toda vez que estivermos avaliando eventos de longo prazo, tomando decisão de negócios onde o período de maturação é longo etc., temos que; levar em consideração este fator.
Segunda lei da Termodinâmica e Risco
Segundo Keynes “ Num tempo relativamente longo todos nós estaremos mortos”
Esta frase é uma certeza determinada pela lei máxima da física que é a segunda lei da termodinâmica.
A segunda Lei da Termodinâmica é a lei vai prevalecer em todas as condições no universo espaço tempo.
Ela estabelece que todo sistema sempre tende ao mais baixo nível de energia, ao longo do tempo, ou seja, tudo vai degradar no tempo.
Por exemplo a corrosão em uma chapa de aço é um bom exemplo, ao longo do tempo a corrosão vai atuar transformando aço em ferro novamente, mais especificamente ferro oxidado.
Podemos dizer em outras palavras que tudo tende a um estágio de maior desordem (entropia) e podemos também afirmar que para construir uma ordem ou estágio de energia mais elevado a energia que vamos dispender para atingir este estágio, parte dela vai ser pedida para atritos e ineficiências do processo. A energia gasta neste processo vai ser maior que a energia final que fica no processo.
Para ficar claro vamos dar um exemplo:
Suponhamos que seja bombeado uma certa quantidade de água numa elevação “h”, a energia necessária para bombear uma certa massa de água “m” a uma altura “h’ é maior que a energia armazenada pela quantidade de água bombeada dada pela equação Ep=mgh, em outras palavras, se formos gerar energia com esta quantidade de água tocando uma turbina a energia gerada será menor que a energia gasta inicialmente para colocar a água na altura desejada.
Resumindo a segunda lei da termodinâmica estabelece que tudo tenderá no tempo a fluir para um nível mais baixo de energia tudo tende ao caos inevitavelmente.
Acidente Zero
Do ponto de vista da segurança tenho visto muitas empresas dizendo que estamos buscando acidente zero. Dentro dos princípios da termodinâmica no tempo longo esta possibilidade não existe, porque considerando que a falta de acidente é uma tendência a ordem e que o acidente é um evento de falha no processo, ou seja, um evento de maior desordem ou caos.
Eu consigo afirmar que um acidente é algo inevitável no longo prazo, probabilisticamente falando.
Considerando um acidente é uma falha no processo de gestão, utilizando softwares de confiabilidade veremos que a distribuição que melhor veste uma base de dados relativos ao histórico de acidentes, é uma distribuição Weibull.
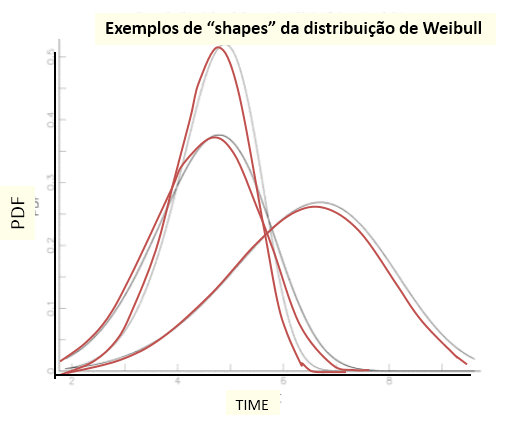
Equação da distribuição Weibull
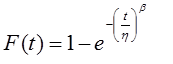
Onde è F= Função da probabilidade no tempo
T= tempo
η = vida característica
Vamos então ver em que condições matematicamente a probabilidade de acidente é igual a “zero”
- Considerando a variável tempo.
A equação vai ter F(t) igual a “Zero”, quando (t/η)=0
Para F(t) ser igual a zero temos duas condições:
- 1 – Para um período de Tempo igual a “Zero”, em outras palavras, isto quer dizer que num tempo muito curto as possibilidades de ficarmos sem acidentes são elevadas e a medida que o tempo vai passando a probabilidade do acidente vai aumentando exponencialmente.
- 2- Outra condição é que F(t) é igual a zero, precisamos obter uma vida característica infinita, neste caso teremos uma probabilidade de acidente “Zero”
Obs:. Vida característica infinita ou eterna, ou mesmo uma vida característica que tenda ao infinito sem falha catastrófica é impossível segundo a lei da termodinâmica, tudo neste universo vai falhar. Não existe nada no universo que seja definitivo inclusive o universo.
Resultado contundente é que, é matematicamente impossível o “ACIDENTE ZERO” num período de tempo muito longo.
Podemos considerar então uma outra abordagem mais plausível, onde acidentes zeros são possíveis em sistemas com taxas de falhas muito baixas num limitado período de tempo!
Vamos então mais na frente ver em que condições vamos ter sucesso num ambiente de risco onde o tempo joga contra, ou seja, que taxas de falhas são aceitáveis internacionalmente num ambiente de risco.
