Histograma

A ferramenta Histograma introduzida no mundo da ciência pelo matemático britânico Karl Pearson no ano de 1895, também conhecida como distribuição de frequências, é utilizada em diversas situação nas escolas e nas empresas. Sua representação gráfica fácil e direta em colunas que marcam como áreas a frequência correspondente à extensão da sua base, ajuda aos estudantes, analistas e gestores em suas respectivas interpretações de fenômenos do seu interesse.
Neste post vamos através da análise do histograma, apresentar conceitos da confiabilidade, matéria muito utilizada na gestão de processos e produtos, especialmente na função manutenção.

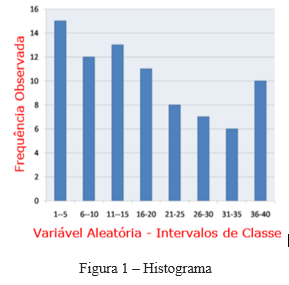
Observando a figura 1, imaginemos que a mesma represente a distribuição de frequências de falha em 8 classes em que as mesmas ocorreram, sendo que tais classes representam faixas de tempo em ciclo de operação do equipamento observado.
A primeira pergunta a ser feita é: qual o banco de dados que gerou este histograma?
A tabela 1 é a fonte, e a mesma representa 50 falhas, onde o analista registrou o ciclo correspondente de cada falha quando a mesma ocorreu (ciclos de operação).

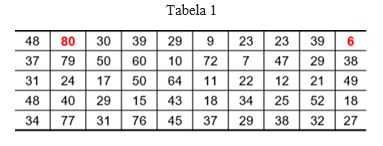
A seguir é preciso organizar os registros das falhas e suas respectivos informações de ciclo de operação no momento da falha. Para tanto é necessário definir a “amplitude do rol (A)”, a “quantidade de classes (K)” e a “amplitude de intervalo de classe (h)”.
O número de classes (K) é dada pela regra de Sturges, que nos traz que K = 1+ 3,3*log(N), onde “N” é o numero de amostras observadas.
Daí, para nosso exemplo, temos: K = 1 + 3,3*log (50) = 6,6 ≈ 7,0 classes.
A amplitude do Rol (A) é a subtração entre o maior valor e o menor valor observado, no exemplo, R = 80 – 6 = 74.
E por fim, a amplitude do intervalo da classe (h), é dado por: h = A / K = 74 / 7 = 10,5 ≈ 11.
Com estes três atributos se tem o histograma, para facilitar sua construção, basta organizar os dados da tabela 1, da forma apresentada na tabela 2.

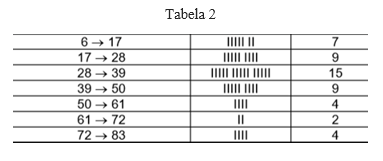Transportando para o histograma temos a figura 2.

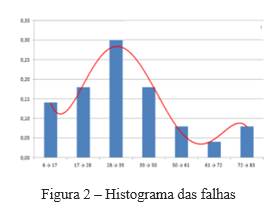
Percebam que a curva em vermelho representa a densidade de probabilidade de falha f(x), a sua equação correspondente, representa o comportamento da probabilidade de falhas de acordo com o tempo, no caso, o número de ciclos de operação.
Ao dividir o número de falhas ocorridas em cada classe pelo total de amostra, temos a frequência relativa simples de cada classe, ao dispô-la de forma acumulativa da classe 1 a 7, obtemos a figura 3, que representa a “probabilidade de falha”, a famosa F(x).

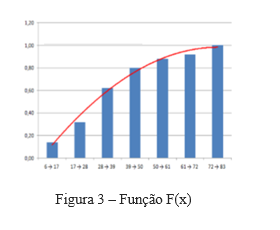
A equação da curva em vermelho consiste na F(x), e como F(x) + R(x) = 1, regra básica da confiabilidade, que diz que a soma das observações que falharam com as observações que obtiveram sucesso é 1, ou 100%, temos que R(x), ou seja, a confiabilidade, é dada por R(x) = 1 – F(x). O que nos leva à figura 4.

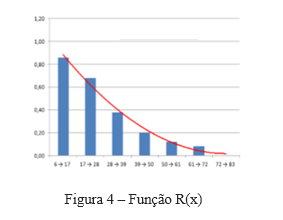
A mesma é o inverso da função F(x), e a curva vermelha representa a confiabilidade do sistema observado.
Os cálculos corretos e precisos de F(x) e R(x) dependem da definição precisa da função f(x), densidade de probabilidade de falha, uma vez que R(x) = 1 – ∫f(x).dx e F(x) = ∫f(x).dx, integrando no intervalo de “0” a “x”.
No entanto, a observação de f(x), F(x) e R(x) através do histograma ajuda, e muito, na observação das curvas de falha e confiabilidade que podem ajudar didaticamente no entendimento dos conceitos pertinentes aos estudos da confiabilidade da manutenção, e consiste nesta dica o objetivo deste post para quem gosta do assunto e está começando a se familiarizar com o mesmo.

 

Post disponível também na pagina do site – Gestão de Operações & Manutenção de Ativos

https://herbertviana.wixsite.com/herbert-viana/single-post/2017/02/19/Aprendendo-conceitos-de-confiabilidade-atrav%C3%A9s-do-histograma